Ovoidul este o curbă plană, închisă, simetrică faţă de o singură axă. Denumire sa provine de la asemănarea ei cu forma unui ou. Construcţia se realizează cu ajutorul a patru arce de cerc după cum urmează:

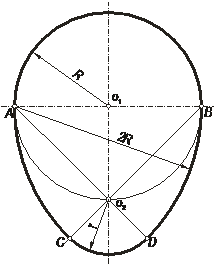
Pe o dreaptă se ia un segment AB ce va constitui axa mică. Mediatoarea lui AB, care trece prin O1, va fi axa mare a ovoidului. Cu vârful compasului în O1 se va trasa un cerc de rază R=AB/2. Se construiesc apoi segmentele AO2 şi BO2, unde O2 este punctul de intersecţie al cercului cu axa mare. Cu vârful compasului în A, respectiv B se vor trasa 2 arce de cerc de rază AB (2R) începând de la B respectiv până la intersecţia lor cu prelungirile segmentelor AO2 şi BO2 .Fie C şi D aceste 2 puncte de intersecţie. Construcţia se termină prin trasarea unui arc de cerc cu centrul în O2 şi rază r = O2C. Forma ovoidală poate fi întâlnită la diferite came sau la profilul canalelor colectoare de canalizare din beton. Un posibil model geometric decorativ compus din forme ovoidale este prezentat mai jos:

Ovalul este o curbă plană închisă simetrică faţă de două axe rectangulare. Construcţia ovalului cu patru centre este prezentată în continuare:

Pe o dreaptă oarecare se ia un segment egal cu axa mare a ovalului. Pe mijlocul acestei axe se ia o perpendiculară care intersectează axa în M. De o parte şi de alta a punctului M se iau segmentele MC = MD egale cu jumătatea axei mici. Pe prelungirea axei MC, se ia un punct E la distanţa MA=MB=ME. Se uneşte apoi punctul C cu punctul A şi cu o deschidere de compas egală cu distanţa CE se trasează un arc de cerc care taie segmentul AC în punctul F. Prin mijlocul segmentului AF se duce o perpendiculară care intersectează axa AB în punctul O1, iar axa CD în O2. Din O2 ca centru şi cu deschidere de compas egală cu distanţa O2C se descrie arcul de cerc care se întinde între prelungirile seg-mentelor O2O3 şi O2O1. Notăm capetele acestui segment cu G şi H. Din centrul O1 cu o rază egală cu O1G se închide sfertul de oval.

Dându-se axa mare a ovalului, construirea lui se face astfel:

Axa mare se împarte în patru părţi egale. Se notează mijlocul axei cu M, iar celelalte diviziuni de pe axă cu O1 şi O3 apoi se descriu două cercuri unul cu centrul în Ol , iar celălalt cu centrul în O3. Razele cercurilor sunt egale O1M = O3M. În continuare din aceleaşi centre O1 respectiv O3, cu o rază egală cu distanţa O1O3 se obţin punctele O2 şi O4, viitoarele centre ale arcelor de închidere a ovalului turtit. Se duc apoi dreptele O1O2, O2O3, O4O3 şi O4O1 şi se notează cu C, D, E şi F punctele în care prelungirile acestor drepte taie cele două cercuri. Acestea sunt punctele de racordare ale celor două cercuri cu arcele trasate din centrele O2 şi O4 conturând astfel ovalul turtit.

Spirala este o curbă plană deschisă care ia naştere prin rotirea unui punct mobil în jurul unui punct fix, folosit ca centru, de care se îndepărtează mereu. Elementele spiralei sunt: spira care este porţiunea din spirală corespunzătoare unei rotaţii complete, pasul spiralei care este distanţa dintre două spire consecutive şi originea spiralei. Există spirale cu două sau mai multe centre alcătuite din arce racordate, care sunt desfăşuratele perimetrelor unor poligoane regulate cu acelaşi număr de laturi.

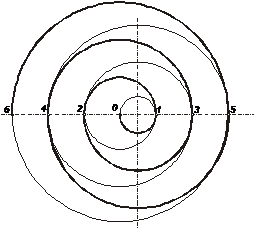
Spirala lui Arhimede
Spirala lui Arhimede este o spirală celebră descoperită de Arhimede, spirală ce poate fi exprimată sub forma unei ecuaţii polare simple. Ea este reprezentată de ecuaţia



Schimbarea parametrului a va roti spirala, pe când b controlează distanţa dintre braţe, care pentru o spirală dată este mereu constantă. Spirala lui Arhimede are două braţe, unul pentru θ > 0 şi unul pentru θ < 0. Cele două braţe sunt conectate la origine şi spirala este derivabilă în acel punct. Luând imaginea în oglindă a unui braţ al său peste linia de la 90°/270° se obţine un alt braţ. Această curbă este notabilă ca una din primele curbe, după secţiunile conice, care a fost descrisă într-un tratat matematic, şi ca prim exemplu de curbă mai bine definită sub formă de ecuaţie polară.

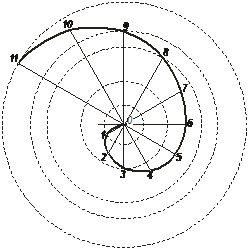
Dându-se originea şi pasul spiralei, se ia ca centru originea dată, apoi cu o deschidere de compas egală cu pasul se descrie un cerc. Acest cerc se împarte într-un număr de părţi egale. Se duc apoi prin cele 12 diviziuni razele prelungite. Din punctul O ca origine pe raza 0,1, se ia lungimea arcului de cerc corespunzătoare lui L/12 şi se obţine primul punct al spiralei. Pe raza 02 se ia această dimensiune de două ori apoi pe razele următoare de 3…12 ori determinându-se astfel cele 12 puncte M1…M12 ale spiralei. Pentru a obţine alura curbei se unesc punctele astfel determinate cu ajutorul florarului. Spiralele se aplică în industrie la construcţia arcurilor, iar dintre spiralele clasice spirala lui Arhimede se aplică la trasarea camelor.

Elipsa este o curbă plană închisă simetrică faţă de două axe rectangulare definită ca locul geometric al punctelor din plan pentru care suma distanţelor la două puncte fixe este constantă.

Trasarea elipsei se face cu compasul în mod aproximativ prin arce de cerc racordate. Metode cunoscute pentru realizarea elipsei sunt: metoda focarelor, metoda benzii de hârtie, metoda construcţiei prin puncte, metoda cercurilor concentrice sau cu ajutorul elipsografului.
În continuare se va descrie metoda cercurilor concentrice:
Fiind date lungimile celor două axe ale elipsei AB şi CD din centrul O se trasează două cercuri concentrice unul având ca diametru axa mică, iar cel de-al doilea axa mare. Prin centrul O se duce un diametru oarecare ce va tăia cercul mic în punctul 1’, iar cercul mare în punctul 1” respectiv 8’ şi 8”. Prin 1’ se duce o paralelă la axa mare, iar prin 1” o paralelă la axa mică. Punctul de intersecţie 1 a celor două paralele duse este un punct al viitoarei elipse. Repetându-se aceste construcţii cu alte diametre se obţin atâtea puncte ale elipsei câte sunt necesare pentru a trasa conturul ei urmând a le uni cu florarul obţinându-se astfel elipsa.

Parabola este o curbă plană deschisă cu o singură axă de simetrie, fiind definită ca locul geometric al punctelor egal depărtate în acelaşi timp de un punct fix numit focar şi de o dreaptă fixă numită directoare. În practică, arcele de parabolă sunt folosite la racordarea muchiilor pieselor precum şi la racordarea liniilor de cale ferată şi tramvai la curbe.

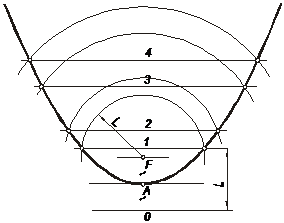
În continuare se va prezenta metoda de construcţie a parabolei prin puncte. Se iau ca elemente iniţiale focarul şi directoarea parabolei. Prin punctul F se duce axa parabolei Ox perpendiculară pe directoarea Δ, iar la jumătatea segmentului FO se fixează vârful A al parabolei. Se iau pe axa Ox câteva puncte arbitrare prin care se duc tot atâtea paralele la directoare. Cu centrul în F şi cu o rază egală cu lungimea segmentului 1,0, se intersectează dreapta dusă prin 1 în punctele 11 şi 12, care aparţin parabolei. Apoi din acelaşi centru, dar cu raza 2,0, se determină alte două puncte 21 şi 22 pe dreapta dusă prin 2. În acelaşi mod se determină celelalte puncte care se unesc printr-o curbă continuă cu ajutorul florarului.

Hiperbola este o curbă plană deschisă alcătuită din două ramuri distincte, având două axe de simetrie rectangulare şi un centru situat la intersecţia axelor. Hiperbola este definită ca fiind locul geometric al punctelor pentru care diferenţa distanţelor la două puncte fixe numite focare situate în planul ei este constantă.

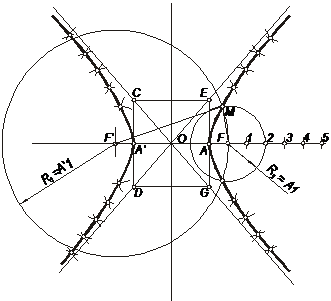
Cele două puncte, fixe focarele F,F', situate la o anumită distanţă între ele numită distanţă focală, se află pe axa orizontală care întâlneşte curba în două puncte AA' numite vârfurile hiperbolei. Cea de-a doua axă nu întâlneşte curba fiind perpendiculară pe axa focarelor şi trece prin mijlocul distanţei focale. Dreptele care unesc focarele cu un punct curent M de pe curbă se numesc raze vectoare. Diferenţa constantă dintre cele două raze vectoare ale aceluiaşi punct de pe hiperbolă este egală cu distanţa AA' dintre vârfurile hiperbolei. Tangenta la curbă într-un punct M coincide cu bisectoarea unghiului făcut de razele vectoare ale aceluiaşi punct.
Se prezintă metoda trasării prin puncte a hiperbolei având date focarele şi diferenţa razelor vectoare. Se dau cele două focare ale hiperbolei F,F' şi un segment AA' egal cu diferenţa razelor vectoare corespunzătoare unui punct M al curbei, egal cu distanţa dintre vârfurile hiperbolei. Din mijlocul O al distanţei focale se ia de o parte şi de alta a axei focarelor câte un segment egal cu jumătatea lui AA' (distanţa dintre vârfurile hiperbolei) determinând astfel vârfurile AA' al curbei.
Pe axa focarelor se marchează poziţia focarului F precum şi câteva puncte arbitrare 1,2,3 etc. Cu centrul în F' luând ca rază segmentul A'1 se trasează un arc de cerc de o parte şi de alta a axei focarelor pe care îl intersectăm cu un al doilea arc de cerc cu raza egală cu segmentul A1 şi având ca centru focarul F.
În acest fel se obţin punctele hiperbolei. Ramura din stânga se obţine modificând ordinea razelor cu care se trasează arcele de cerc din cele două focare. Asimptotele hiperbolei sunt două drepte concurente în centrul O şi tangente în punctele de la infinit ale curbei.
Tangentele la hiperbolă în vârfurile A şi A' ale curbei sunt paralele cu axa verticală. Dacă prin punctele de intersecţie cu asimptotele ale celor două tangente duse prin A şi A' se duc paralele la axa orizontală se obţine un dreptunghi (CE,DG) care are drept laturi lungimile axelor hiperbolei şi diagonalele după asimptotele acesteia. Hiperbola pentru care dreptunghiul axelor devine un pătrat se numeşte hiperbolă echilateră.

Este curba descrisă de un punct M, aparţinând unui cerc C, ce se rostogoleşte fără alunecare pe o curbă fixă Δ

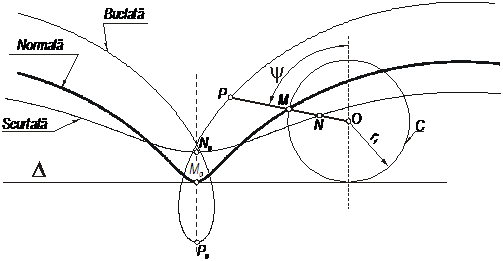
După poziţia punctului fix M faţă de cercul generator se mai pot genera ortocicloide buclate sau alungite atunci când punctul generator P legat de cercul C se află în exteriorul acestuia  şi ortocicloide scurtate atunci când punctul generator N legat de cercul C se află în interiorul acestuia.
Dacă punctul generator ajunge să coincidă cu centrul cercului, N≡O, ortocicloida scurtată devine o dreaptă paralelă cu dreapta Δ.
Ecuaţiile parametrice ale ortocicloidei sunt:

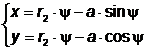
unde a reprezintă distanţa de la punctul generator la centrul O al cercului C.
Dacă
a < r2 , se obţine ortocicloida scurtată,
a = r2 , se obţine ortocicloida normală,
a > r2 , se obţine ortocicloida buclată.

Hipocicloida este curba descrisă de un punct M aparţinând unui cerc C2 care se rostogoleşte fără alunecare pe un cerc fix C1.

În afară de hipocicloida generată de punctul M, mai pot fi generate hipocicloide buclate atunci când punctul generator P legat de cercul C se află în afara acestuia şi hipocicloide scurtate atunci când punctul generator N legat de cercul C se află în interiorul acestuia.
Când N≡O2, hipocicloida scurtată degenerează într-un cerc cu centrul în O1. Ecuaţiile parametrice ale hipocicloidei sunt: ,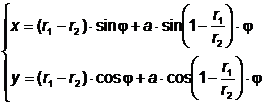
unde a reprezintă distanţa de la punctul generator la centrul cercului O2.
Dacă
a < r2 , se obţine hipocicloida scurtată,
a = r2 , se obţine hipocicloida normală,
a > r2 , se obţine hipocicloida buclată.

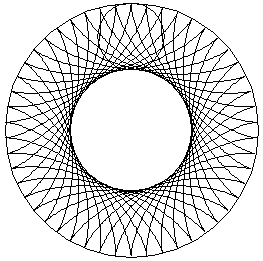
Dacă raportul dintre diametrele celor 2 cercuri este un număr raţional curba nu se “închide” după parcurgerea unui cerc complet. Astfel pot fi create figuri de genul celei alăturate unde cercul mic parcurge 23 de rotaţii pe cercul mare.

Epicicloida este curba descrisă de un punct M aparţinând unui cerc C2 care se rostogoleşte fără alunecare pe un alt cerc fix C1. În afară de epicicloida normală generată de punctul M se mai pot genera epicicloida buclată generată de punctul P care este legat de cercul C2 situat în afara acestuia şi epicicloida scurtată atunci când punctul generator N, legat de C2 este în interiorul acestuia.

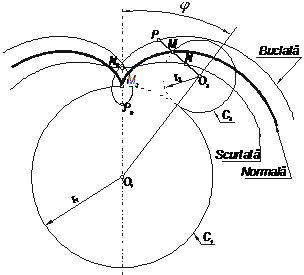
Când N≡O2 epicicloida scurtată  devine cerc cu centrul în O1 şi de rază r1+r2.Ecuaţiile parametrice ale epicicloidei sunt:


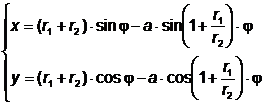
unde a reprezintă distanţa de la punctul generator până la centrul cercului O2.
Dacă
a < r2 , se obţine epicicloida scurtată,
a = r2 , se obţine epicicloida normală,
a > r2 , se obţine epicicloida buclată.

Dacă raportul dintre diametrele celor 2 cercuri este un număr raţional curba nu se “închide” după parcurgerea unui cerc complet. Astfel pot fi create figuri de genul celei alăturate unde cercul mic parcurge 47 de rotaţii pe cercul mare până punctul generator ajunge în poziţia de pornire.

Pericicloida se asemănă ca mod de generare cu hipocicloida cu deosebirea că cercul mic rămâne fix, iar cercul mare se rostogoleşte, tangent interior, la cel mic.

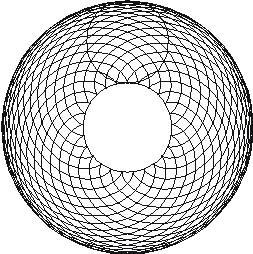
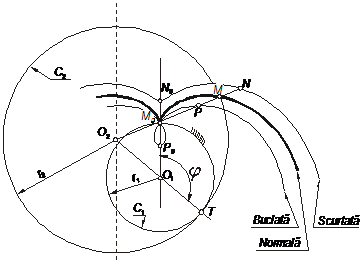
Astfel pericicloida este curba descrisă de un punct M aparţinând unui cerc C2 care se rostogoleşte fără alunecare pe partea interioară pe un cerc fix C1.
În afară de pericicloida normală  generată de punctul M de pe cercul C2 se mai pot genera pericicloide buclate atunci când punctul generator P legat de C2 se află în interiorul acestuia şi pericicloide scurtate atunci când punctul generator N legat de C2 se află în exteriorul acestuia. Ecuaţiile generatoare ale coordonatelor carteziene ale punctului curent sunt:

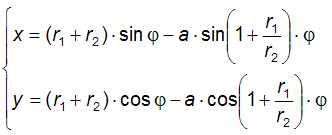
unde a reprezintă distanţa de la punctul generator până la centrul cercului O2.
Dacă
a < r2 , se obţine epicicloida scurtată,
a = r2 , se obţine epicicloida normală,
a > r2 , se obţine epicicloida buclată
Deşi ele sunt identice cu ale hipocicloidei, se observă că notaţiile de pe desen diferă corespunzător poziţiei fixe a cercului mic şi mobile a cercului mare.
Dacă raportul dintre diametrele celor 2 cercuri este un număr raţional curba nu se “închide” după parcurgerea unui cerc complet.


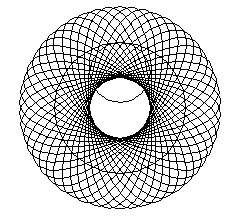
Astfel pot fi create figuri de genul celei de mai sus unde cercul mare parcurge 33 de rotaţii pe cercul mare până punctul generator revine în poziţia de pornire.

Evolventa de cerc este curba descrisă de un punct M aparţinând unei drepte Δ care se rostogoleşte fără alunecare pe un cerc de rază r numit cerc de bază. Evolventa are două ramuri cu punctul de întoarcere M0 aflat pe cercul de bază. În afară de evolventa normală generată de punctul M ce se află pe dreapta Δ se mai pot genera evolvente buclate atunci când punctul generator P este legat de dreapta Δ, dar în afara ei şi anume spre centrul O şi evolvente scurtate atunci când punctul generator N este legat de dreapta Δ, dar în afara ei şi anume în exterior faţă de O.


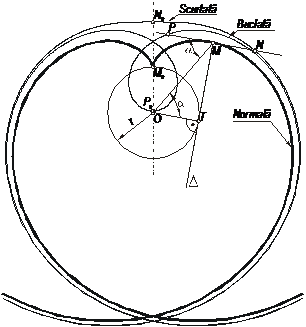
Dacă  MP = r  atunci evolventa buclată va trece chiar prin O devenind în acest caz spirala lui Arhimede.
Din teoria mecanismelor unghiul α se numeşte unghi de presiune, el modificându-şi valoarea în diferitele puncte ale evolventei.
Ecuaţiile parametrice ale evolventei sunt:



unde a reprezintă distanţa de la punctul generator până la dreapta Δ.
Dacă
a > 0 , se obţine evolventa scurtată,
a = 0 , se obţine evolventa normală,
a < 0 , se obţine evolventa buclată, a = - r, se obţine  spirala lui Arhimede.